什么是自然数（什么是整数）

节选自《数学极客：探索数字、逻辑、计算之美》, 已获机械出版社授权许可, [遇见数学] 特此表示感谢!

当你想到数学的时候，首先映入脑海的多半是数字。数字具有非常神奇的吸引力。但是，当你深入地思考数字是什么时，你会吃惊地发现，我们中的大多数人对它知之甚少。

如何准确定义数字？什么样的数字是实数？或者说，什么是实数？有多少数字？有多少种不同类型的数字？

我不可能告诉你所有关于数字的知识，这些知识可以写20～30本书。但是，我可以带你开启一段数字之旅，给你介绍数字的基本知识，然后一起看看一些奇异和有趣的数字。

▌第1章　自然数

什么是数字？

在数学中，我们可以从几个角度来回答这个问题。我们可以从语义的角度回答，即数字的含义是什么。或者，我们可以从公理的角度回答，即数字是怎样定义的。或者，我们也可以从构造的角度回答，即数字是怎样从一些简单对象构造而来的。

我们从语义开始，数字的含义是什么？每个人都认为自己知道这个问题的答案，而大多数情况下，他们都错了！大家觉得数字只是一个计数的工具，但是这并不符合事实。根据不同的使用场景，数字有两种不同的含义。

有两种类型的数字。当看见数字3的时候，你并不能真正理解它的含义。数字3可以有两种不同的含义，所以当你不知道你在使用其中哪个含义时，它是多义性的。数字3可以是我有三个苹果里的3，也可以是我得了第三名里的3。三个苹果里的3是基数，而第三名里的3是序数。

基数记录了一组物体的数量。当我说我想要三个苹果时，3是一个基数。序数记录了一个物体在一组物体里面的排名。当我说我想要第三个苹果时，3是一个序数。在英语里，这个区别很明显，因为英语有一种序数的语法形式。three是基数，third是序数。它们在语法上就不一样，因而可以非常明显地看出哪个是基数哪个是序数。

从数学的集合论基础说起，才会发现基数和序数的真实区别。第16章会详细地介绍集合论。现在，我们只需要知道一个基础的概念：基数用来记数，序数用来定位。

公理定义的数字更加有意思。在公理化定义中，我们看到的是一些规则的集合，称为公理。公理定义了数字（或者你要定义的其他概念）需要遵守的规则。在数学上，我们总是倾向于公理化定义，因为公理化定义可以消除所有的多义性。公理化定义不够直观，但是绝对精确，并且可以用作形式化推理的依据。

数学是美丽的，它既有趣又令人兴奋，同时也很实用。本书探讨了两千多年的数学发展历程中一些伟大的突破和有趣的话题：从埃及分数到图灵机，从数字 的真正意义到证明树、群对称和机械化计算。如果你想知道高中几何课中难以完成的证明背后到底隐藏着什么，或者什么限制了计算机的能力，本书将会带你找到答案。

▌1.1　自然数的公理化定义

我们将从一组基础的数字说起：自然数。自然数（记为N）是大于等于0且没有小数部分的数字。

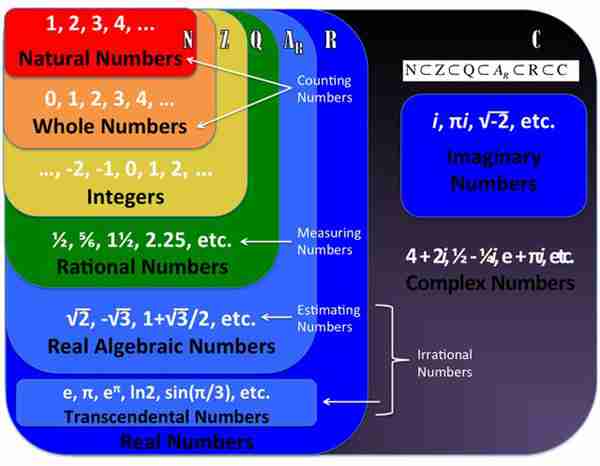
当你说到数字的时候，通常是指自然数，因为自然数是最基础的数字。自然数是我们小时候最先接触的数字。自然数是从0开始的整数，没有小数部分，一直增大到正无穷：0,1,2,3,4，;（像我这样的计算机科学家对自然数总是情有独钟，因为所有可计算的事物都可以用自然数表示）。

事实上，自然数是由称为皮亚诺算术（Peano arithmetic）的一组规则定义的。皮亚诺算术使用几个公理来定义自然数。

初始值规则：0是一个特殊的自然数。

后继规则：对于任何一个自然数n，总是存在称作它后继的另外一个自然数s(n)。

前继规则：0不是任何自然数的后继，除了0以外的任何自然数都是某个自然数的后继，这个数称为前继。如果有两个自然数a和b，如果b是a的后继，那么a就是b的前继。

唯一性规则：任意两个自然数不能有相同的后继。

相等规则：自然数可以进行相等比较。这条规则有三条子规则：自反性，即每个自然数都和它自身相等；对称性，即如果a=b，那么b=a；传递性，即如果a=b，b=c，那么a=c。

归纳规则：对于某个陈述P，我们说P对于全部自然数是真的，如果

1.对于自然数0，陈述P是真的（记作P(0)是真的）。

2.如果对于某个自然数n，陈述P是真的（即P(n)是真的），那么你能证明陈述P对n的后继s(n)也是真的（即P(s(n))是真的）。

所有这些规则只是自然数是从0开始的没有小数部分的整数的一种更加新潮的说法。大部分人第一眼看到皮亚诺规则的时候，会觉得这些规则除了最后一条之外还是很容易理解的。归纳法是一种颇具技巧性的思想。我知道，在我第一次看到归纳证明时，我肯定没有明白它的本质，我感觉被循环绕进去了，被弄得晕头转向。但是，归纳是必不可少的：因为自然数是一个无限的集合，所以只有当我们能够以某种推理将有限扩展到无限时，才能说某个陈述关于这个无限的集合是真的。归纳的任务就是将有限对象延伸推理到无限集合。

当你熟悉了公理的形式后，归纳法真正想说的是：存在某种你可以使用的模式。如果你有一个适用于第一个数字的定义，那么就可以通过一个加1操作将其推理到所有其他的数字。通过这样的模式，你能证明对于所有自然数这个定义是正确的。或者，可以写出适用于所有自然数的定义。我们可以在所有整数、小数或者实数上使用相似的技巧。

与证明相比，定义更简单，因此在试图证明前，我们将先写定义。我们来看一个将归纳法应用到定义证明的例子。我们来看看加法，很容易给出自然数加法的定义。加法是两个自然数的求和，用符号+表示。加法的正式定义满足如下性质：

交换性：对任意一对自然数n和m，n+m=m+n

恒等性：对任意自然数n，n+0=0+n=n

递归性：对任意自然数m和n，m+s(n)=s(m+n)最后一条规则就是归纳规则，并且通过递归的方式实现。因为当你不习惯用递归时，递归比较难，所以我们先不急于展开。

我们正在做的是通过皮亚诺算术里的后继规则来定义加法。如果使用+1和-1重写，等式是很容易理解的：m+n=1+(m+(n-1))。

为了理解，你只需要记住这是一个定义而不是一个程序。因此，这是在描述加法的含义，而不是怎么做加法。

由于皮亚诺的归纳规则，这里的最后一条规则才起作用。否则，我们该如何定义两个数字做加法的含义？归纳法给了我们一个描述任意两个自然数做加法的方法。

现在轮到证明登场了！对大多数人来说，证明往往很吓人，但是不要担心。证明其实并没有那么可怕，我们将做一个非常简单的证明。(待续)