毛球定理是什么(毛球定理怎样发现的)

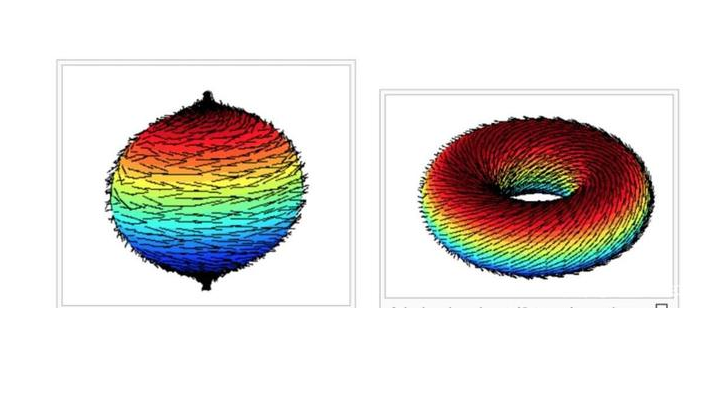
　　毛球定理是一项有趣而重要的代数拓扑定理，它描述了在三维球面上不存在连续且处处不为零的切向量场。这个定理的直观理解是，无法将一个球面上的毛球抚平，即无法找到一个连续的向量场，使得它在球面的每个点都与球面相切且不为零。这个定理的证明和推广对于理解流形的性质和拓扑学的发展具有重要意义。

　　一、毛球定理的内容和直观理解

　　毛球定理的内容可以简单概括为：在三维球面上不存在处处连续的非零并且与球面相切的向量场。这意味着无法在球面上找到一个连续的向量场，使得它在球面的每个点都与球面相切且不为零。这个定理最早由鲁伊兹·布劳威尔在1912年证明。

　　直观上理解，我们可以将球面上的向量场想象成一团毛球，其中每根毛发代表一个向量，而球面上的每个点都与球面相切。毛球定理告诉我们，无论如何抚平这个毛球，总会存在一个点无法被抚平，即无法找到一个与球面相切且不为零的向量。这个定理的直观理解也可以用气象学中的气旋来解释，气旋的中心即为球面上的一个零点，而气旋周围的风则形成一个螺旋形的分布。

　　二、毛球定理的证明和推广

　　毛球定理的证明可以通过数学推理和拓扑学的方法进行。证明的关键在于利用欧拉示性数和庞加莱-霍普夫定理。根据庞加莱-霍普夫定理，三维空间中的向量场的零点处的指数和为2，即二维球面的欧拉示性数。因此，根据欧拉示性数的性质，二维球面上的连续切向量场必然存在至少一个零点。而对于偶数维的球面，其欧拉示性数为2，因此也必然存在至少一个零点。

　　毛球定理还可以推广到更高维度和更多的流形上。对于任意的正则的偶数维紧流形，若其欧拉示性数不为0，则其上的连续的切向量场必然存在零点。这个推广对于理解流形的性质和拓扑学的发展具有重要意义。

　　三、毛球定理的应用

　　毛球定理在数学和物理学中有着广泛的应用。在数学领域，毛球定理是拓扑学中的一个重要定理，它揭示了流形的性质和向量场的存在性。在物理学中，毛球定理可以应用于气象学中对气旋的研究。通过将大气运动看作地球表面的向量场，毛球定理可以解释为什么气旋的中心处风平浪静，而周围则有风环绕。